Tupper's Formula • The Applied Go Weekly Newsletter 2025-05-11

Your weekly source of Go news, tips, and projects

Tupper's Formula: A formula that calculates itself as a bitmap image

Hi ,

How about an entertaining detour into mathematics? No worries, it won't get too abstract. But this formula I'm going to show you in the Spotlight is just too fascinating: It can calculate any 17x160 bitmap image you can imagine—including an image of the formula itself! It all depends on where the y coordinate starts. Sounds weird, but the formula isn't overly complicated and can be implemented with a few lines of Go.

Maths can be funny sometimes.

–Christoph

Featured articles

Graceful Shutdown in Go: Practical Patterns

Don't bring your car to a halt by crashing into a wall, and don't exit your Go web app without properly finishing pending requests and releasing resources.

Build your own ResponseWriter: safer HTTP in Go - Antonio Pitasi

The default implementation of http.ResponseWriter contains some pitfalls for the unprepared user. Luckily, ResponseWriter is an interface, so you can write an alternative implementation. Antonio shares his approach.

[security] Go 1.24.3 and Go 1.23.9 are released

Go 1.24.3 and 1.23.9 are released, fixing a vulnerability in os.Root that allows accessing the parent directory of Root.

(Download directly from go.dev/dl or through your favorite OS package manager.)

Podcast corner

Fallthrough: The Language of Data Visualization

Do you know decksh? I must admit that I didn't ... until this Fallthrough episode. decksh is a language that Anthony Starks designed for creating slides declaratively, without Powerpoint or the like, and without unnecessary "language noise".

Cup o' Go: Metal! 🤘 Bare metal go, config libs, building response writers

This is hot sh*t: How about compiling Go code to bare metal? Like, no OS between the app and the hardware. The Tamago project is about to get "upleveled" and have their bare-metal OS target become an official one.

Spotlight: Tupper's "self-referential" formula

In this week's Spotlight, I want to look at a deeply mathematical yet playful topic.

Take a look at the following formula:

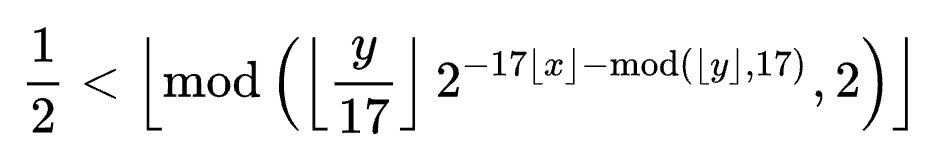(All images in this text are taken from Wikipedia, licensed under CC-BY-SA.)

Looks quite wild doesn't it? No worries, you don't have to understand the formula in detail. The interesting part is what it does:

For given x and y, the formula determines whether to set a pixel at the coordinates (x,y) to black or white, depending on whether the result of the right side is less than, or greater or equal to, one half.

Ok, so what?

Bear with me. There is a really fascinating aspect to this formula. You might expect that this formula prints some graph that's interesting for mathematicians but boring like heck for the rest of us.

What the formula actually does sounds pretty unbelievable: It can output virtually anything that you can describe as a 17x106 black-and white picture.

How so? The secret is a large number k that doesn't appear in the formula itself. Instead, k determines the starting point for y. So we're moving along the y-axis to generate, no: calculate any 17x106 b/w image we want.

As you can imagine, k can become pretty large! Take, for example, this k value:

960 939 379 918 958 884 971 672 962 127 852 754 715 004 339 660 129 306 651 505 519 271 702 802 395 266 424 689 642 842 174 350 718 121 267 153 782 770 623 355 993 237 280 874 144 307 891 325 963 941 337 723 487 857 735 749 823 926 629 715 517 173 716 995 165 232 890 538 221 612 403 238 855 866 184 013 235 585 136 048 828 693 337 902 491 454 229 288 667 081 096 184 496 091 705 183 454 067 827 731 551 705 405 381 627 380 967 602 565 625 016 981 482 083 418 783 163 849 115 590 225 610 003 652 351 370 343 874 461 848 378 737 238 198 224 849 863 465 033 159 410 054 974 700 593 138 339 226 497 249 461 751 545 728 366 702 369 745 461 014 655 997 933 798 537 483 143 786 841 806 593 422 227 898 388 722 980 000 748 404 719

If you feed the formula with x and y value by iterating x from 0 to 105 and y from k to k+17, the formula generates the following plot:

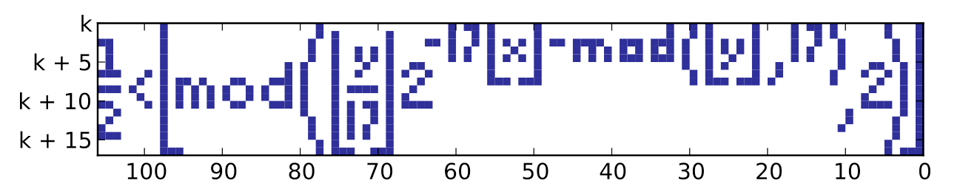
Holy mackerel! You just need to find a suitable k to make the formula plot itself! (That's why it's often called "Tupper's self-referential formula", BTW.)

But in fact, finding k is not difficult, it's just a bit tedious if you do it manually. In fact, you can construct a k for any 17x106 bitmap image you like!

The steps are:

1. Create a 17x106 bitmap image of your choice.
2. Go through the image column by column. Start at (0,0) in the upper right corner (note that in the bitmap screenshot, the x-axis runs from right to left, and the y axis from top to bottom!) and go down the first column, then down the second column, and so forth.
3. For each pixel visited, note down a white pixel as 0 and a black pixel as 1.
4. Repeat until you arrive at the final pixel. Now you have a pretty long binary number.
5. Convert the binary number into a decimal number and multiply it by 17—that's your k.

These steps uncover the secret behind Tupper's formula. The value k encodes a bitmap, and as it is used as the seed value for y, the formula can reconstruct each pixel by "reversing" the encoding.

I let Eli Bendersky explain the details of the formula and move right on to implementing Tupper's formula in Go! As there are fairly large numbers involved, math/big is our only bet for evaluating Tupper's formula.

Note that the methods of type big.Int expect pointers to big.Int; that's why you see quite a few NewInt() and new(big.Int) calls in the function that implements the formula:

func tupperMatrix(kconst *big.Int) [17][106]bool {
    var tmatrix [17][106]bool

    // Pre-allocate constants outside the loop
    bigOne := big.NewInt(1)
    bigTwo := big.NewInt(2)
    big17 := big.NewInt(17)

    // Pre-allocate variables for reuse
    y := new(big.Int)
    a := new(big.Int)
    b := new(big.Int)
    temp := new(big.Int)
    powResult := new(big.Int)

    for i := range 106 {
        for j := range 17 {
            y.Add(kconst, big.NewInt(int64(j)))
            a.Div(y, big17)
            b.Mod(y, big17)
            temp.SetInt64(int64(i))
            temp.Mul(temp, big17)
            b.Add(b, temp)
            powResult.Exp(bigTwo, b, nil)
            a.Div(a, powResult)
            a.Mod(a, bigTwo)
            // Store result in matrix (flipped horizontally)
            tmatrix[j][105-i] = a.Cmp(bigOne) == 0
        }
    }

    return tmatrix
}

The reason is that big.Int values can become arbitrarily large, only capped by the available main memory (and swap space). Shuffling them around on the stack could thus become quite inefficent. Hence, pointers.

The rest of the code only needs to call tupperMatrix() and print out the result, using block characters for better appearance. (It's not as nice as a real bitmap, for the typical monospace fonts have no square characters, and add spacing between characters and lines.)

func main() {
    k := new(big.Int)
    _, success := k.SetString("960939379918958884971672962127852754715004339660129306651505519271702802395266424689642842174350718121267153782770623355993237280874144307891325963941337723487857735749823926629715517173716995165232890538221612403238855866184013235585136048828693337902491454229288667081096184496091705183454067827731551705405381627380967602565625016981482083418783163849115590225610003652351370343874461848378737238198224849863465033159410054974700593138339226497249461751545728366702369745461014655997933798537483143786841806593422227898388722980000748404719", 10)

    if !success {
        fmt.Println("Failed to parse the k constant")
        return
    }

    bmap := tupperMatrix(k)

    for _, line := range bmap {
        for _, col := range line {
            if col {
                fmt.Print("█") // Unicode block character
            } else {
                fmt.Print(" ")
            }
        }
        fmt.Println()
    }
}

Here is the Playground version. Feel free to try out different values of k. To generate a k from an image, you can find k generators online, such as Tupper's Self-Referential Formula Playground.

Hat tip to who brought my attention to this formula through an article in Spektrum der Wissenschaft 6.25.

For an entertaining introduction to Tupper's formula, watch The 'Everything' Formula from Numberphile, in which Matt Parker demonstrates the formula and how to construct k. (I'm still not sure if this is just a camera trick or if Matt is actually capable of writing down k from the top of his head!)

Quote of the Week: The hard part of making software

Coding is not the hard part of making software. People are the hard part of making software.

Therefore, computer science is a humanities study.

–Maaike Brinkhof

More articles, videos, talks

Lets build MapReduce from Scratch - by venkat - Just Build

The concept of MapReduce is fairly simple, the implementation—not so much. Venkat implements a minimal MapReduce system from scratch to explore its inner workings.

HiveGo - Hive game and AI implemented in Go

Even if catching the queen of a beehive isn't your thing, the repo contains some interesting technical background information about the ingredients of this AI-powered game.

Real-Time database change tracking in Go: Implementing PostgreSQL CDC

How to track PostgreSQL database changes in real time through Change Data Capture (CDC).

Projects

Libraries

GitHub - sonirico/gozo: A practical Go toolkit with generic utilities for working with slices, maps, and functional programming primitives like Option and Result.

If you think samber/lo, you're quite close. The author of this library plans to add more functionality, though.

GitHub - doganarif/GoVisual: Zero-config, pure-Go HTTP request visualizer & debugger for local Go web development.

Inspect HTTP requests in a convenient Web UI.

Tools and applications

Conduit | Data Integration for Production Data Stores

Developers in need of a data streaming services probably reached out to Redpanda Connect, formerly known as Benthos. Now there's a new contender on the market: Conduit.

gomultirate package - github.com/Gustavo-Feijo/gomultirate - Go Packages

What if a 3rd-party API imposes two different rate limits at the same time? Such as, 20 requests per second and 100 requests per two minutes.

This library manages multiple rate limits for your application, ensuring your app doesn't get penalized by the 3rd-party API.

GitHub - tienanr/docurift: DocuRift is an intelligent API documentation generator that automatically analyzes your API traffic and generates comprehensive documentation in multiple formats. It works as a proxy server that captures API requests and responses, then generates OpenAPI and Postman collection documentation.

Have some badly documented, or even undocumented APIs? This tool proxies connections and builds an OpenAPI spec from the requests that travel by.

GitHub - Sriram-PR/doc-scraper: Go web crawler to scrape documentation sites and convert content to clean Markdown for LLM ingestion (RAG, training data).

Important feature: The scraper respectsrobots.txt.

Completely unrelated to Go

There's Beauty in AI

...but only if you know how to wield this tool.

Reservoir Sampling

Another article by Sam Rose (Sam who?) with tons of fine animations to help the reader understand why reservoir sampling is needed and how it works.

(Even if you don't care a bit about reservoir sampling, you WILL enjoy the graphics and diagrams, trust me!)

Happy coding! ʕ◔ϖ◔ʔ

Questions or feedback? Drop me a line. I'd love to hear from you.

Best from Munich, Christoph

Not a subscriber yet?

If you read this newsletter issue online, or if someone forwarded the newsletter to you, subscribe for regular updates to get every new issue earlier than the online version, and more reliable than an occasional forwarding. 

Find the subscription form at the end of this page.

How I can help

If you're looking for more useful content around Go, here are some ways I can help you become a better Gopher (or a Gopher at all):

On AppliedGo.net, I blog about Go projects, algorithms and data structures in Go, and other fun stuff.

Or visit the AppliedGo.com blog and learn about language specifics, Go updates, and programming-related stuff. 

My AppliedGo YouTube channel hosts quick tip and crash course videos that help you get more productive and creative with Go.

Enroll in my Go course for developers that stands out for its intense use of animated graphics for explaining abstract concepts in an intuitive way. Numerous short and concise lectures allow you to schedule your learning flow as you like.

Check it out.

Christoph Berger IT Products and Services
Dachauer Straße 29
Bergkirchen
Germany